Magnetic trapping of neutral atoms has become an important technique for reaching ultra-low temperatures in dilute gases of atoms. Since the temperature and density limits associated with laser cooling are absent in magnetic traps, high phase-space densities can be achieved through evaporative cooling. This has made possible, among other things, the experimental realization of Bose-Einstein Condensation (BEC) in a gas of alkali atoms. Magnetic traps fall into two different categories: Static traps, such as the Ioffe-Pritchard trap and its derivatives, and dynamic traps, also known as time-orbiting-potential (TOP) traps. The key point of both the static and the dynamic traps is to eliminate the zero of the magnetic field at the centre of the trap, which leads to Majorana spin-flips in which the atoms are transferred into untrapped states and hence lost. The TOP-trap solves this problem by adding a rotating homogeneous magnetic field to the quadrupole field creating the trap. This shifts the zero of the magnetic field away from the centre, and if the frequency of rotation is large enough, the atoms on average experience a static harmonic potential. The zero of the magnetic field now orbits the centre of the trap, creating a “circle of death” which can be used in order to effect evaporative cooling. Although it is clear that the static harmonic potential the atoms see is only an approximation, and despite the fact that theoretical studies have predicted important corrections to this approximation, little experimental work has been done in order to verify these predictions. Experimental results on a Rb condensate have demonstrated the presence of dynamical phenomena beyond the usual approximations applied to TOP-traps1.
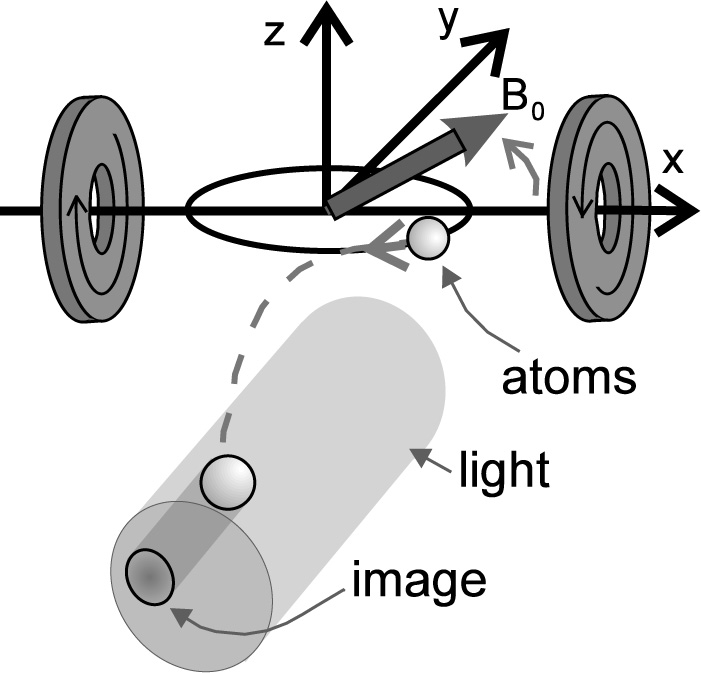
In our TOP trap a homogeneous magnetic bias field is superposed on a quadrupole field (gradient b') with the direction of the bias field of magnitude B0 rotating at angular frequency w0 in a plane containing the symmetry axis of the quadrupole coils, Fig. 1. In this case the resulting TOP-trap is called triaxial because the cylindrical symmetry of the quadrupole coils is broken, resulting in three different harmonic frequencies of the trap.

Figure 1
In order to describe analytically the motion of atoms in a TOP-trap, two approximations are usually made. The first, also called the adiabatic approximation, concerns the orientation of the atomic magnetic dipole with respect to the local direction of the magnetic field. As the atom moves and the magnitude and direction of the local field change, the magnetic moment of the atom will precess around the direction of the field, and if the field changes too fast (notably when going through zero), Majorana spin-flips can be induced. In the adiabatic approximation, then, it is assumed that the Larmor precession frequency of the magnetic dipole is much larger than the rotational frequency of the bias field, and hence the magnetic dipole can be thought of as being aligned with the local field at all times. In this case, the interaction energy between the magnetic moment m and the total magnetic field (quadrupole plus bias field) is simply m Btot.
The second approximation, which we shall call the `time-averaging' approximation, is based on the assumption that the frequency of oscillation of the atoms in the (to first order) harmonic potential created by the superposition of the quadrupole and bias fields is much smaller than the frequency w0 of the bias field. The atoms will, therefore, experience many periods of the bias field before appreciably changing their position. This allows one to average over a whole period of the bias field at a fixed position of the atoms, leading to a time-averaged potential in the adiabatic approximation2. When gravity is included, this measurably influences both the equilibrium position and the vibrational frequencies in the trap.
When the time-averaging approximation is lifted in the description of the atomic motion in a TOP-trap, the atoms experience a time-dependent potential at frequency w0 and its harmonics. We therefore have observed a modulation of the velocity of the atoms at w0. In order to verify that there is, indeed, a modulation at w0 of the velocity of the BECs in the TOP-trap, we had to monitor this quantity at different phases of the TOP-cycle. Thus we were able to switch off the trapping fields in a time that is short compared with the period of the rotating bias field. If this was not the case, the atoms see a slowly decreasing trapping field over several cycles of the rotating bias field, which will wash out the effects of the micromotion. Our apparatus allows us to switch off the quadrupole field in less than 20 ms, which is short compared with the period of 100 ms of the bias field. After a time-of-flight a few milliseconds the vertical position of the condensate is determined using absorption imaging of the atomic cloud. From this measurement and the position of the condensate immediately after switching off the trap (determined in the same way), the velocity component along the x-axis can be found. We have clearly seen the vx oscillating around 0 with the period of the bias field, with the maxima of the velocity occurring when the bias field points along or against the direction of observation. No such variation was found on the position of the atoms. Indeed, a simple calculation shows that for a typical micromotion velocity amplitude of 5 mm/s, the expected spatial amplitude is of the order of 100 nm, which is well below our resolution limit of about 5 mm. When the sense of rotation of the bias field was reversed, the phase of the measured velocity was shifted by 180 degrees, in accordance with the physical picture of the atoms being `dragged' along by the instantaneous position of the quadrupole centre.
The second approximation of the TOP-trap is the adiabatic approximation. Although the effect of lifting this approximation is not as intuitively obvious as the micromotion appearing when the time-averaging approximation is dropped, we can get a feel for the consequences through the following argument. As long as we assume that the spin (and hence the magnetic moment) of the atom is always aligned with the B-field, the fact that the Larmor precession of the atomic spin has a fixed direction that only depends on the internal degrees of freedom of the atom does not come into play. In other words, whether the bias field rotates clockwise or counterclockwise should not make an observable difference because of symmetry considerations. If the Larmor precession is included, however, the problem acquires a handedness, and we can now distinguish between the two senses of rotation of the bias field since the Larmor precession defines a preferred direction. It turns out that this manifests itself as a difference in the equilibrium position along the vertical axis of the atoms in the trap for the two opposite senses of rotation of the bias field, as schematically described in Fig. 2.

Figure 2
In order to determine precisely the equilibrium position of the atoms in the TOP-trap, we excited small oscillations of the condensate after the adiabatic expansion by applying briefly, for about 2 ms (i.e. much shorter than the typical oscillatory periods of 20-100 ms in these particular experiments), a magnetic field along the z-axis which gave a kick to the atoms. Thereafter, the position of the condensate was measured at various delays. A sinusoidal fit to the position data then yielded both the oscillation frequencies and the equilibrium position of the atoms. This experiment was repeated with the sense of rotation of the bias field reversed. We took great care in ensuring that when the sense of rotation of the bias field was reversed, all other parameters of the experiment remained unaltered. To achieve this, we used two phase-locked function generators andchanged their relative phase by 180 degrees to reverse the sense of rotation. Fig. 3 shows typical results of such a set of experiments. One clearly sees the splitting Dzeq, which we were able to determine to within 3 mm. For large quadrupole gradients the measured splitting Dzeq presents a linear dependence on 1/b', whereas for the smallest gradients the splitting data deviate significantly from a straight line as b' approaches the minimum gradient, b'=15.3 G/cm, necessary to balance gravity.
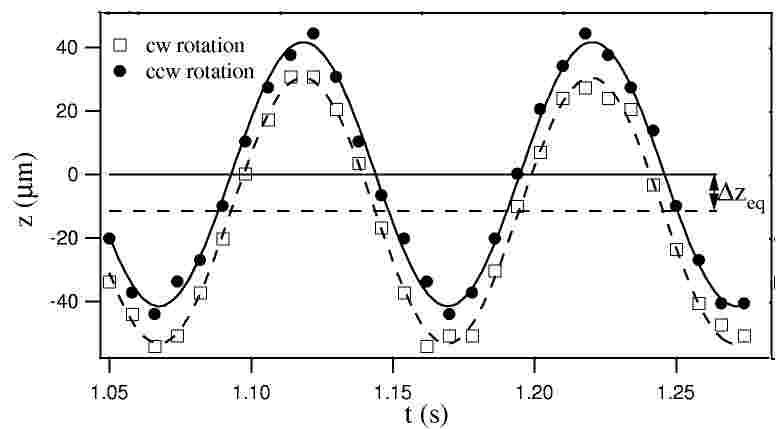
Figure 3
The experimentally observed phenomena are small corrections to the secular motion of cold atoms and condensates in a TOP-trap. Nevertheless, they can conceivably be important under various circumstances. In experiments where accurate control over the condensate residual motion is required on the recoil scale (5 mm/s), for instance, it is important to take into account the micromotion velocity to avoid systematic errors. This can be the case in atom lasers or in the transfer of a condensate into a different kind of trap (e.g. an optical lattice or a dipole trap).
The present experiment has provided direct evidence of the geometric forces acting on atoms moving in an inhomogeneous magnetic field. Within the area of cold atoms the role of geometric forces has already been taken into account for atomic motion in the magnetic field created by a wire, although no direct evidence for such forces was found experimentally. We should like to point out here that the phenomena reported in the present work do not require a Bose-Einstein condensate. We used condensates mainly because their small size greatly facilitated precise position measurements. Experiments with evaporatively cooled but uncondensed thermal clouds yielded the same results within the experimental uncertainty.